Model of Allocating Public Financial Resources to Brazilian Hospital Organizations that Provide Highly Complex Health Care Services
Abstract
The general objective of this paper was to propose a model of allocating public financial resources to Brazilian hospital organizations that provide highly complex health care services on behalf of the Brazilian Unified Health System (SUS). The main theoretical background was built on Carr-Hill et al. [1] Focusing on the highly complex health care services provided by the hospitals, the study underscored factors such as supply (or productivity and accessibility/availability of services/beds), demand (or need for health care), use (or utilization/consumption of services/beds), and complexity segmentation of the service in Brazil. The sample comprised 251 organizations offering at least type-II adult and type-II newborn Intensive Care Units in 23 Brazilian states and classified as general and/or specialized hospitals. The Carr-Hill et al. [1] model was adapted to propose a simplified theoretical model of supply that could represent the relationship between the variables included in the final equation of the model, namely: mean inpatient cost, availability of basic health care services, bed occupancy rate, organization type, and organization nature. The results pointed out that the significant determinants empirically confirm the arguments that are rejected by sanitarians in the theoretical field – that the model of resource allocation is based on productivity.
INTRODUCTION
The need to allocate the (scarce) health care resources more relationally was already pointed out by Feldstein, Piot and Sundaresan [2] some decades ago. Today, Espírito-Santo, Fernando and Bezerra [3] share a similar perspective and claim that the structural problems of the public health care system are, to some extent, related to resource allocation.
In Brazil, the 1988 Federal Constitution [4] created the Unified Health System (SUS) to ensure the right to universal and integral access to health care. However, full access to SUS has not been granted so far because of the organization of the health care service network and the current system of resource allocation to the health care organizations.
This study addresses this issue, focusing on the resource allocative efficiency of the network of hospitals that offer highly complex health care services (i.e., health care services that require high technology equipment and inpatient admission in an ICU) within the Brazilian Unified Health System (SUS). In other words, it focuses on how resource allocation is related to the supply of highly complex health care services. A Brazil-specific model built on Carr-Hill et al. [1] was created to explain the allocation of financial resources to SUS hospital organizations that provide highly complex health care services.
The model approaches particularly the costing of such services, that is, the (in)sufficiency of financial resources
that SUS has to disburse to pay off the costs that public hospitals and/or certified private hospitals incur while providing highly complex services. This may, however, also be interpreted as a limitation of this study, as it does not include a direct analysis of the amount of resources needed for investments. Other limitations are related to the modeling per se, derived from the original shortcomings of the Carr-Hill et al. [1] model and that of its adaptation to the Brazilian case.
Following the Carr-Hill et al. [1] model, this study differentiates the several types of services (e.g., non-psychiatric, outpatient services, and public health care). Drawing on Bloor and Mayner [5], this differentiation derives from the understanding that each of such types of services requires a different volume of resources and, therefore, has a different impact on the public budget. Since the computation and analysis of costs are based on the observed expenses, that is, those already incurred, it follows that it is a contradiction to accept the current system of service supply and the current health care policy as adequate, despite the criticisms made against them [6].
REFERENCE MODEL AND NECESSARY ADAPTATIONS
Mendes, Leite and Marques [7] agree with Porto [8] that the international model of resource allocation most applicable to the Brazilian case is that built on the English experience, the Resource Allocation Working Party 2 model (RAWP-2). Porto [8] claims that an adaptation of the RAPW-2 model, as proposed by Carr-Hill et al. [1], is the most statistically robust and theoretically grounded model to date. This model allows for measuring relative inequalities that are much less significant than those observed in Brazil and, if adjusted, could be adequately adopted in the country [7].
This study assumes the Carr-Hill et al. [1] model as a theoretical reference to identify and analyze the determinants of a financial resource allocation model for Brazilian hospital organizations that provide highly complex health care services within the SUS framework. Some adaptations and reservations apply, however, to the model developed in this study.
First, the Carr-Hill et al. [1] model includes specific criteria for each expense item before resource distribution. In other words, the theoretical model distinguishes the different complexity levels of health care services (low, medium, and high) and accounts for the socio-demographic and per capita differences of a population. This study, however, is limited to the highly complex services.
Second, the model’s applicability required the adaptation of some items. The variables and classification system of organizations were adapted, instead of reproducing the original model’s applicability to regions and/or federated state. The Carr-Hill et al. [1] model’s orientation was also adapted to replace the focus on the needs (demand) for health care service with a focus on reorganizing the hospital network according to productive capacity associated with availability of resources and service supply (production/utilization). Instead of being the model’s focus, the estimation of needs was one of the variables used to allocate resources.
METHODOLOGY
This study includes general hospitals (5,193) and specialist hospitals (1,088) listed in the National Database of Health Facilities (CNES). This database provides the hospital’s location (state/municipality) and type of available beds (whether or not they are devoted to SUS): surgical beds, examination beds, intermediate/intensive care beds, delivery beds, beds for other specialties, and hospital-day beds.
This study only included the general and specialist hospitals that admit patients to intensive care units (ICUs), as it focuses on the highly complex health care services. The initial sample encompassed all 1,105 hospitals and their 18,329 SUS beds, including: adult ICUs - types I, II, and III; pediatric ICUs - types I, II, and III; neonatal ICUs - types I, II, and III; burn ICUs; and coronary ICUs - types II, and III).
To reduce the great variability of ICU beds, the sample was limited to type-II adult and newborn ICU beds, which, together, corresponded to nearly 70% of the initial sample. This criterion led to 266 hospital organizations, but 2 of them were excluded because they were classified as ambulance stations.
Thirteen other organizations were excluded because of the lack of segregated data for all variables. In the end, the sample consisted of 251 organizations listed in the CNES as either general hospitals (234) or specialist hospitals (17), all of which have at least type-II adult and newborn ICU beds. Together, these organization offer 6,170 ICU beds. The data refer to year 2012 and were collected from DATASUS (SUS databank), CNES, and reports by IBGE (Brazilian Institute of Geography and Statistics) and RIPSA (Interagency Network of Health Information).
This sample was used to either corroborate or refute the following hypotheses:
- H1: Supply is a function of demand and use;
- H2: Use is a function of demand and supply;
- H3: Determinants of use of general hospital beds are demand variables;
- H4: Determinants of use of specialist hospital beds are supply variables; and
- H5: The most used hospitals (i.e., those with the highest number of admissions) are those that supply more (i.e., those with the highest occupancy rates).
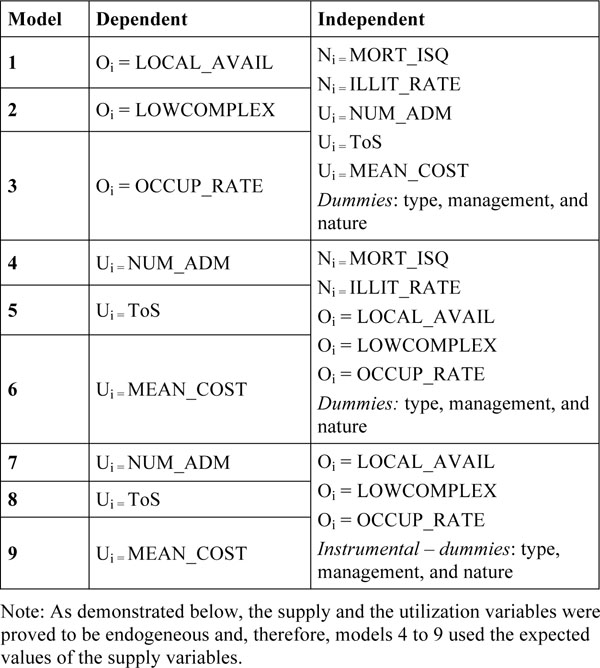
These hypotheses were tested using a combination of the different variables included in this study and in nine models (see Fig. 2). Following the work by Carr-Hill et al. [1], the general objective of the formulations was to identify possible determinants for each combination of variables, with a view to reaching a “final” resource allocation model.
The initial modeling included the following quantitative variables, which fall into the three categories proposed by Carr-Hill et al. [1] (i.e., utilization, need, and supply):
- Utilization: number of admissions (NUM_ADM), Mean Time of Stay (ToS), and Mean Cost of Autho-rized Hospital Admissions (AHA) (MEAN_COST);
- Need (or demand): (1) health condition, based on mortality by ischemic heart diseases Group ICD-10 (MORT_ISQ); and (2) socio-economic conditions, based on the illiteracy rate (ILLIT_RATE); and
- Supply: (1) of hospital services – proxy local accessi-bility/availability (% local patients admitted to the hospital) (LOCAL_AVAIL); (2) of primary care – proxy 1/number of low complexity services (LOW-COMPLEX), and proxy 1/family health care teams (FHT) (which provide low and medium complexity services); and (3) of hospital beds – occupancy rate (OCCUP_RATE).
The utilization variables employed in this study are theoretically equivalent to those used in Carr-Hill et al. [1] The need variables, however, are adaptations of two of the three dimensions of demand proposed by Carr-Hill et al. [1] (demography, health condition, and socio-economic conditions).
Unlike the Carr-Hill et al. [1] procedures, this study did not include some demographic variables (sex and age), as it neither standardizes the data according to basic cause of disease (ICD) nor compares local/regional with national/federate results. The reason is two fold: (1) the study included only organizations with ICUs that provide highly complex services (considered according to the ICD), which demand patient admission for treatment; and (2) the hospital organizations were understood as members of a national network of SUS services, which implies it would be incoherent to compare locations/regions.
As in the original RAWP model, Carr-Hill et al. [1] standardized the variables based on the demographic variables of sex and age, aiming at differentiating the specific needs according to basic cause of disease and population group (male/female, and age group) at the local/regional level as compared to the national/federated level. Carr-Hill et al. [1], however, admit that such a standardization does not eliminate a demographic effect on the variables used in the model. Therefore, this study aimed at first aggregating the resources allocated to the SUS ICU beds for non-psychiatric admissions in general, regardless of the ICD of the services, that is, all admissions in ICU beds were included in the model, regardless of the basic cause of disease. The study also assumed that providing highly complex services, which imply admission in ICU beds, requires substantial infrastructure and high-technology equipment.
Because of this specificity and disregarding the basic cause of disease, the availability and demand for such beds are barely determined by the local demographics (i.e., sex and age), considering the flow of patients moving from one region to another seeking highly complex services. In other words, no matter the demographics of the municipality in which a hospital is located, it is expected to admit patients from other regions/municipalities, meaning that the hospital’s availability and demand will not always be consistent with the municipality’s demographics. In addition, this study did not consider the supply of highly complex services at the regional/local level because it assumed that SUS’s public hospitals and certified private hospitals are part of a national network of health care services.
The supply variables in this study are also adaptations of those used by Carr-Hill et al. [1]. Such variables revolve around the notion of perceived accessibility or availability and refer to the following measures according to the authors: (1) access to hospital services; (2) access to health care; (3) availability of home care; and (4) access to beds in private hospitals. These supply variables were adapted as: (1) access to hospital services (LOCAL_AVAIL); (2) access to primary care (LOWCOMPLEX and FHT); and (3) access to hospital beds (OCCUP_RATE).
The primary care variables included a proxy of the number of low complexity services as a measure of accessibility/availability. The assumption was that a higher number of such services corresponded to a greater level of follow-up of the patients’ health state, which would incidentally reduce the number of “avoidable” admissions, all of this implying a greater availability of hospital beds. The assumption is similar to another proxy measure, one related to the number of family health care teams (FHT): the greater the number of such teams, the greater the number of low/medium complexity services, which would correspond to a greater level of follow-up of the patients’ health state and a consequent reduction in the number of “avoidable” admissions, all of this implying a greater availability of hospital beds. As one can see, these two proxy variables are inversely related to the availability of highly complex services.
The study also included qualitative variables, represented by dummy variables, to classify the hospital organizations, namely: type of hospital unit (TYPE), type of management (MGMENT), and organization nature (NAT). TYPE (dummy 1, or D1) refers to either general hospital (D1 = 0) or specialist hospital (D1 = 1). MGMENT is characterized as follows: (1) D2 = 1 for state-level management, otherwise D2 = 0; (2) D3 = 1 for municipality-level management, otherwise D3 = 0; (3) D4 = 1 for management at both levels, otherwise D4 = 0. NAT (dummy 5, or D5) refers to either a private organization (D5 = 0) or a public organization (D5 = 1). According to CNES, private organizations include collectively-owned hospitals, private companies, non-profit organizations, and private foundations, while public organizations include government health agencies (health ministry, state and municipal health departments) and other areas (education ministry, navy, etc.), as well as other public agencies (mixed-economy agencies, civilian employers, public foundations, and public/social partnerships).
To be more specific, sample in this study mostly comprises general hospitals (234 vs 17 specialist hospitals) and private hospitals (136 vs 115 public hospitals). For this reason, D1 = 0 was used to refer to general hospitals as a part of variable TYPE and D5 = 0 to refer to private hospitals as a part of variable NAT.
After defining the variables building on an adaptation of the Carr-Hill et al. [1] model, this study proposes a simpli-fied theoretical model of supply (Fig. 1), which represents how the variables are related to one another, including those derived from the hypotheses presented in Methodology Section.
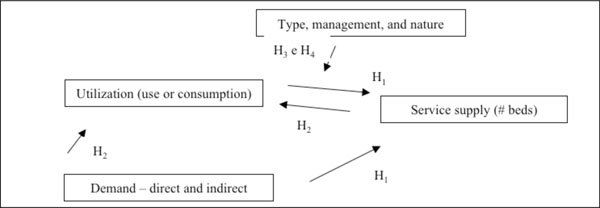
Simplified theoretical model of supply.
The nine models were estimated with a view to identifying the significant variables within each group of variables (i.e., supply, demand, use, and classification). In other words, the aim was to identify the variables that could be used in a final resource allocation model for Brazilian companies providing highly complex health care services within the SUS network.
Three analyses were carried out following the Carr-Hill et al. [1] proposal. The authors recommend a correlation analysis as a first step toward a preliminary selection of the variables to be included in the model. Once the model has been formulated, the following step is to perform endogeneity and heteroscedasticity tests to assess the need to use the two stage least square to estimate the models’ parameters.
The correlation analysis was based on Pearson’s correlation tests of the variables according to group (supply, demand, and utilization) with a view to identifying the ones that could be included in the estimated models (see Fig. 2). The endogeneity tests resulted in no endogeneous variables and, therefore, all models in this study were estimated using the original values of the supply variables, as suggested by Carr-Hill et al. [1]
Estimated models.
The method of least squares was also considered as a method to estimate the regression parameters in the absence of endogeneity. Otherwise, the two stage least square method would be more suitable, as recommended by Carr-Hill et al. [1]
Despite following the same estimation sequence, this paper is, to some extent, different from that proposed by Carr-Hill et al. [1] and used in Porto et al. [9] in a study that aimed to test/adapt the Carr-Hill et al. [1] model to the Brazilian case. Not only does this paper adopt a different model orientation, but it also focuses on a resource allocation model for hospital organizations, rather than administrative regions [1] and/or federated units [9]. Consequently, the analysis does not compare values allocated according to region/federated unit with values at the national level.
All models estimated in this study (see Fig. 2) consist of linear regressions, as proposed in Carr-Hill et al. [1], and the greatest relevance of the formulations herein proposed lies not in the modeling itself (partial combination of variables), but rather in the complementarity of the correlation analyses of the variables that will compose a “final” model. That was the reason for not having performed a test for correct specification of the model, which is commonly used in linear regression models to identify relevant variables that are absent or unnecessarily included in the model.
In addition, this type of model (i.e., a linear regression model) usually relies on using the method of least squares to estimate the parameters. Nevertheless, as Carr-Hill et al. [1] point out, the two stage least square method is the one most recommended in the absence of endogeneity between the supply and utilization variables. In this study, no endogeneity was found between the supply and utilization variables and, therefore, both estimation methods were used for the regression parameters: (1) the two stage least square method, as suggested by Carr-Hill et al. [1] ; and (2) the method of least squares.
A special note should be given to the task of identifying heteroscedasticity. Since Carr-Hill et al. [1] do not suggest a specific method to overcome heteroscedascity in the estimated models, all heteroscedastic models were excluded in the present analysis, namely models 1 and 3 (see Fig. 2). Other tests related to classic linear regression models were carried out in addition to that of heteroscedasticity, namely for: absence of heteroscedasticity, independence of residuals (or non-autocorrelated residuals), and absence of multicollinearity. One should also notice that a classic linear regression model does not involve any hypotheses about residual distribution. It only requires that the residuals’ mean values should be zero and their variance should be a finite constant.
Problems of heteroscedasticity and autocorrelation indicate that the method of least squares is inefficient to estimate the parameters and, therefore, this method was ruled out when these issues came out, such as in model 1 (see Fig. 2). If only autocorrelation applied, the two stage least square method was used, as in models 4 and 7 (see Fig. 2). If multi-collinearity applied, the method of least square was used because the parameters of such a test still remain as the best unbiased linear estimators.
MODEL FORMULATION FOR THE BRAZILIAN CASE
The models formulated for the Brazilian case fall into three groups (see Fig. 2). Two of the groups (4 to 6, and 7 to 9) have utilization variables as the dependent variables. These variables represent: how much the organization spends (MEAN_COST) on highly complex services provided within the SUS network; the volume of use of SUS beds, as accounted by the number of SUS patients’ admission (NUM_ADM), and the time of use of the services, based on the number of patients admitted and discharged (ToS).
The only model in which utilization was not included as a dependent variable is model 2, which had LOW-COMPLEX, a supply variable, as the dependent variable. As the aim of estimating the models was to support an analysis of resource allocation determinants and equate a “final” model for the Brazilian case, the results displayed in Fig. (3) include only the variables with statistical significance in each model (p<0.05).
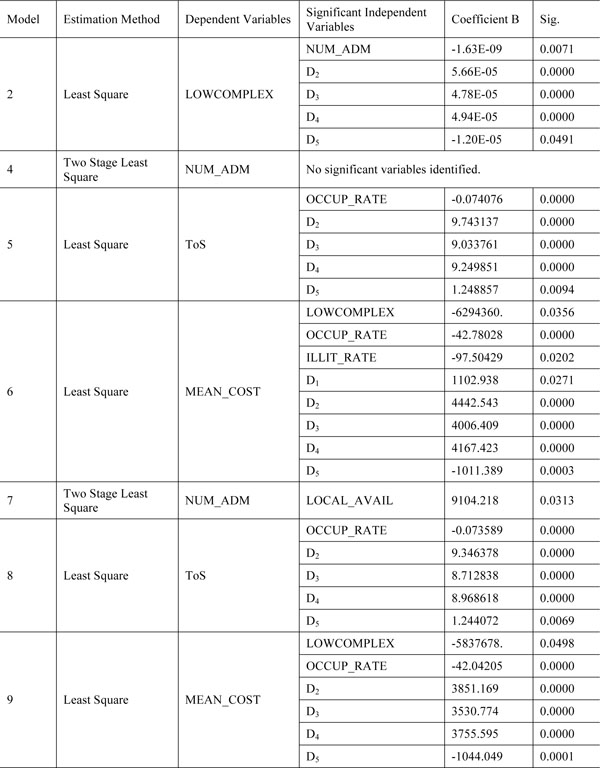
Significant variables in models 2 and 4-9.
As this figure shows, no significant variables were found for model 4, estimated using the two stage least square method. Fig. (3) also shows that all three MGMENT variables (dummies 2 to 4) were statistically significant conjointly, which, however, has no explanation in the literature and runs counter the initial expectation that at least one of these variables was individually significant, indicating that the type of management (at the state level, at the municipal level, or at both levels) would explain the low or high use of the services.
As mentioned, two of the groups of models (4 to 6, and 7 to 9) have utilization (MEAN_COST, NUM_ADM and ToS) as the dependent variable. The only model in which utilization was not included as a dependent variable is model 2, which had LOWCOMPLEX, a supply variable, as the dependent variable. As the aim of estimating the models was to support an analysis of resource allocation determinants and equate a “final” model for the Brazilian case, the results displayed in Fig. (3) include only the variables with statistical significance in each model (p<0.05).
ANALYSIS OF THE DETERMINANTS OF THE MODELS
In model 2, NUM_ADM and dummies 2-5 were statistically significant (p<0.05) (see Fig. 3). As previously mentioned, the group of models 1-3 was aimed at identifying which variables could explain the supply of services at Brazilian hospital organizations. According to the result of model 2, the variables that explain the supply – more specifically, the access to low complexity services (LOWCOMPLEX) – are NUM_ADM and the hospital classification variables MGMENT (dummies 2-4) and NAT (dummy 5).
Mafra [10] reported a negative relationship between primary care and the number of admissions for highly complex services in Brazil. According to the author, primary care reduces the need for long-term or inpatient treatments. As shown in Fig. (3), LOWCOMPLEX and NUM_ADM are negatively related, as the independent variable’s coefficient is negative.
However, LOWCOMPLEX is a proxy variable calculated as follows: 1/number of low complexity services. It follows that, holding all other variables constant, the lower LOWCOMPLEX, the higher the number of low complexity services/appointments. Considering this, a positive relationship was expected between LOWCOMPLEX and the utilization variable NUM_ADM, that is, it was expected that the lower LOWCOMPLEX is and, therefore, the higher the number of low complexity services is, the lower the use of highly complex services would be. In other word, NUM_ADM would be lower, as suggested in Mafra [10]. This relationship was not confirmed in the second model.
Furthermore, dummy variables 2-5 in model 2 also explain the access to low complexity services (LOWCOMPLEX). The following can be reproduced for the MGMENT variables (dummies 2-4): all three variables were statistically significant, but no explanation for that has been reported in the literature.
The relationship is negative for variable NAT (dummy 5): the public nature of the hospital organizations (D5=1) explains the reductions in variable LOWCOMPLEX and, therefore, the number of low complexity services. This result seems to corroborate the current health care policy in Brazil, which prioritizes low complexity services [11].
In the second group of models, no significant need variables were identified in models 4 and 5, but ILLIT_RATE was negatively related to MEAN_COST in model 6.
In model 5, the supply variable OCCUP_RATE and the classification variables (dummies 2-5) explain the utilization variable ToS. According to the results, OCCUP_RATE is negatively related to ToS, that is, holding all other variable constant, the greater the utilization (ToS), the lower the supply (OCCUP_RATE). This result is not only coherent in practice (i.e., greater use, lower availability), but also seems to theoretically corroborate Silva et al. [12]. The authors state that low mean time of stay (low ToSs) may imply not only increased productivity, but also early discharges, pre-mature deaths, or avoidable deaths (or higher OCCUP_ RATEs).
Moreover, dummy variables 2-5 in model 5 also explain the utilization of services (ToS) and are positively related to this variable. As for MGMENT variables (dummies 2-4), no justification was found for their conjoint statistical significance. Variable NAT (dummy 5) had a direct relationship with ToS, which indicates that the public nature of the hospitals (i.e., D5=1) explains the increased utilization of highly complex services. As the analysis of the study hypotheses will show (see Fig. 4), public hospitals had, on average, higher NUM_ADMs and ToS. This result seems to corroborate McCue and Nayar [13], according to whom private (and for-profit) hospitals have better performances and tend to have a lower rate of admissions and lower ToS.
In model 6, supply (LOWCOMPLEX and OCCUP_ RATE), need (ILLIT_RATEG), and hospital classification (dummies 1-5) explain utilization (MEAN_COST). This was the only model that pointed to need variables with statistical significance. This result seems to corroborate the unders-tanding that the Brazilian model of resources allocation is based on productivity (supply), rather than on demand (need). Other results, as reported below, support this claim.
Variables according to hospital type and nature.
Specifically, the need variable ILLIT_RATE is negati-vely related to MEAN_COST, unlike the classification variables, which are positively related to utilization in model 6. The supply variables, in turn, are negatively related to utilization, which indicates that the higher the utilization (MEAN_COST), the lower the supply (LOWCOMPLEX and OCCUP_RATE).
A note should be given to the specific computation of LOWCOMPLEX, that is, 1/number of low complexity services. The results in model 6 confirmed the expectation that, holding the other variables constant, the lower LOWCOMPLEX is, the higher the number of low complexity services is, and, following Mafra [10], the lower the number of admissions for highly complex services, which, therefore, implies higher inpatient costs.
The negative relation between OCCUP_RATE and MEAN_COST corroborates Barnum and Kutzin [14], according to whom a greater OCCUP_RATE tends to result in lower costs per patient (or per admission), because the total (direct and indirect) costs are distributed across the beds that are usually occupied.
The negative relationship between utilization (MEAN_COST) and need (ILLIT_RATE) in model 6 consistently and theoretically indicates that the greater the use of low complex health care services, the lower the need for highly complex health care services. In other words, lower illiteracy rates indicate a greater need for highly complex services and, theoretically, more use of such services.
The same applies for the classification variables as it does for the MGMENT variables (dummies 2-4): the three variables have statistical relevance, but so far the literature has no explanation for it. In contrast, the variable TYPE (general or specialist hospital – dummy 1) is positively related to MEAN_COST, indicating that the medical specialty of an organization consistently explains higher MEAN_COSTs. The reason is that specialized health care services are more expensive, since they require high-technology equipment and technical and operational facilities that are adequate to take care of serious and complex health issues.
Variable NAT (dummy 5) is negatively related to MEAN_COST in model 6, that is, the public nature (D5=1) of a hospital organization explains low MEAN_COSTs. Schuhmann [15] states that private (and for-profit) hospitals have lower OCCUP_RATEs, lower ToS, and lower costs. In other words, the results in this study refute those provided by this author. This may be related to the sample considered in the present study.
Most of the hospitals herein analyzed (131 out of 251) are general private organizations (i.e., D1=0 e D5=0), while the remaining are general public hospitals (103), public specialist hospitals (12), and private specialist hospitals (5). In general, building on Porter and Teisberg [16] and on Christensen [17], a way to (re)organize the network of highly complex health care services would be to segment it into: (1) public general hospitals providing public services for low complexity cases; and (2) private specialist hospitals, which require more investments given the specialized services provided. It follows that private hospitals (TYPE) were expected to be matched to specialized hospitals (NAT). Although the number of private general hospitals in this study’s sample is representative, the literature provides no explanation to this result, that is, that the public nature (D5=1) of the hospital organizations explains the low MEAN_COSTs.
The three last models, 7 to 9, aimed at assessing whether a lower or greater utilization of the services would be determined/explained by the supply and classification of the organizations. Models 7 to 9 are an adaptation of the final demand model proposed by Carr-Hill et al. [1] and an operationalization of the simplified theoretical model of supply set forth in this study (see Fig. 1).
In model 7, estimated using the two stage least square method, only LOCAL_AVAIL was statistically significant. This variable is positively related to the dependent variable (see Fig. 3), indicating that, holding all the other variables constant, the greater the supply (LOCAL_AVAIL), the greater the utilization (NUM_ADM). Unlike the other relationships obtained in the other models of the third group (models 7-9), this relationship points to the possible existence of induced demands. In other words, the more services a patient gets, the more he/she seeks health care services.
In model 8, the relationships between the dependent and independent variables are the same as those in model 5. That is, the independent supply variable OCCUP_RATE is negatively related to the dependent utilization variable ToS in both models 5 and 8. Furthermore, the dummy variables 2-5 also explain utilization and are positively related to it. The analysis of the determinants in both models are, therefore, similar.
Both in model 5 and model 8, the negative relationship between OCCUP_RATE and ToS indicates that, holding all the other variables constant, the lower the utilization (ToS), the lower the supply), which corroborates Silva et al. [12] Once again dummies 2-4 are statistically significant conjointly, but no explanation could be found for this. Variable NAT (dummy 5) had a direct relationship with ToS in both models 5 and 8, which indicates that the public nature of the hospitals (i.e., D5=1) explains the increased utilization of highly complex services, thus corroborating Schuhmann [15].
In model 9, supply (LOWCOMPLEX and OCCUP_ RATE) and hospital classification (dummies 1-5) explain utilization (MEAN_COST). Similar to model 6, the supply variables in model 9 are negatively related to utilization, which indicates that the greater the utilization (MEAN_ COST), the lower the supply (LOWCOMPLEX and OCCUP_RATE). In other words, in both models, holding the other variables constant, the results confirm the expectation that the lower LOWCOMPLEX is, the higher the number of low complexity services is, and, following Mafra [10], the lower the number of admissions for highly complex services, which, therefore, implies higher inpatient costs. A negative relationship between OCCUP_RATE and MEAN_COST, in turn, corroborates Barnum and Kutzin [14].
Once again, the conjoint significance of three classification variables MGMENT (dummies 2-4) finds no explanation in the literature. Variable NAT (dummy 5) is negatively related to MEAN_COST in both models 6 and 9, that is, the public nature (D5=1) of a hospital organization explains low MEAN_COSTs.
TEST OF HYPOTHESES AND THE FINAL MODEL
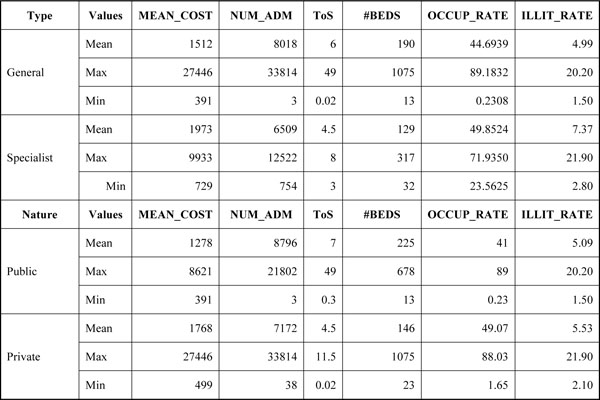
To test the hypotheses, the following was considered in addition to the analysis of the determinants in the models: (1) some values refer to utilization variables MEAN_COST, NUM_ADM and ToS, to the variables #BEDS, OCCUP_RATE and ILLIT_RATE, and to classification variables TYPE and NAT, as shown in Fig. (4); and (2) Porter and Teisberg’s [16] and Christensen’s [17] understanding of general and specialist hospitals.
In the sample (251 hospitals), 17 organizations (7%) were categorized as specialist hospitals. As Fig. (4) shows, compared to the 234 general hospitals, the specialist hospitals’ values are discrepant only in relation to the maximum number of hospital admissions (NUM_ADM): 33,814 vs 6,509. However, the mean number of hospital admissions are relatively close: 8,018 vs 6,509.
The mean inpatient costs (MEAN_COST) are also close between general and specialist hospitals, and also between public and private hospitals: 1,512 vs 1,913, and 1,278 vs 1,768 respectively. ToS is another variable with close results between both types of hospitals: on average, 6 vs 4.5 days for general and specialist hospitals respectively. However, general hospitals kept inpatients for 49 days at most, while the specialist hospitals kept them for eight days. Another observation concerns the maximum number of hospital beds: the sample has general hospitals with 1,075 available beds at most vs 317 in specialist hospitals. However, the mean number of hospital beds is once again relatively close: 190 in general hospitals vs 129 in specialist hospitals.
Building on such results as well as on model 6, it is possible to see that the significance of variable TYPE as a way to explain CUST_UMED with a positive relation indicates that high mean inpatient costs (MEAN_COST) are usually incurred in specialist hospitals. Nevertheless, as shown in Fig. (4), the volume of hospital admissions (NUM_ADM) is lower at specialist hospitals.
Such differences may be consistent with the specialist hospitals’ physical and technological infrastructure as well as their qualified workforce. The supply of specialized health care services seems to explain a tighter structure than that of general hospitals, which usually provide health care services in a number of medical specialties. In addition, the more specialized a treatment is, the more expensive it is.
As for the organizations’ nature, there is a relationship between the mean values of #BEDS and ToS. The public hospital had, on average, greater #BEDS and ToS than the private hospitals, which, in turn, had greater productivity (OCCUP_RATE) and volume of utilization (NUM_ADM). This seems to explain the practice of certifying and/or contracting private hospitals to meet the demand for health care services that is not met by public organizations. Nevertheless, a note should be given to the similar ILLIT_RATEs in the municipality where the analyzed organizations are located, which seem to have no relationship with productivity according to the organization’s nature.
Building on such considerations and the analysis of the significant variables obtained in each of the estimated models, it is possible to assess the hypotheses put forward in the Introduction. The first hypothesis (H1) refers to the relationship between the supply, demand, and utilization variables. It is not possible to either confirm or refute such a hypothesis building on the determinants in the first group of models (1-3). This is particularly relevant in model 2, in which the dependent variable LOWCOMPLEX was only significantly related to NUM_ADM.
The second hypothesis (H2), that utilization is a function of demand and supply, was confirmed by model 6, according to which the independent supply variables LOWCOMPLEX and OCCUP_RATE and the independent demand variable ILLIT_RATE were significantly related to utilization. This model seems to corroborate the expectation of adapting the Carr-Hill et al. [1] model. In other words, model 6 indicates the possibility of at least replicating the Carr-Hill et al. [1] proposal. Moreover, model 6 confirms the theoretical model’s expectation (Fig. 1) that utilization is a function of demand and supply.
Indirect empirical deductions were also made to either confirm or refute hypotheses 3 and 4 (H3 and H4), as the number of specialist hospitals in the sample was not large enough for robust linear regression analyses.
In model 6, the variable TYPE was significant to explain utilization (MEAN_COST) on a positive relationship basis, indicating that the hospital’s specialty explains its increased use of services. Additionally, as mentioned in the analysis of Fig. (4) in this section, higher MEAN_COSTs (utilization) take place in specialist hospitals, which also have higher OCCUP_RATEs (supply). This seems to indicate that the supply variables are related to variable TYPE, but no determination relationship could be confirmed between them. Consequently, it was not possible to either confirm or refute H4.
As for hypothesis 3 (H3), only model 6 pointed to statistical significance for a demand variable, namely ILLIT_ RATE. As previously mentioned, the negative relationship between utilization (MEAN_COST) and need (ILLIT_ RATE) indicates that places with lower illiteracy rates are those with the greater need for highly complex health care services and, theoretically, those with the greater utilization of such services.
In addition, the analysis in Fig. (4) also reveals that the higher the illiteracy rate (ILLIT_RATE), the higher NUM_ADM is in the municipality where the hospital is located. The reason is that general hospitals are located in municipalities with lower ILLIT_RATEs than those where the specialist hospitals are located. In other words, it seems that greater numbers of admissions occur, on average, in general hospitals located in municipalities with low ILLIT_ RATEs, that is, utilization is negatively related to need. Consequently, the results obtained in model 6 and the indirect analysis of the data in Fig. (4) seem to indicate that the use of beds in general hospitals is somehow related to demand variables, but not determined by them. Therefore, it was not possible to either confirm or refute H3.
As for the fifth hypothesis (H5), the results are inconclusive as to whether the most frequently used hospitals (with higher NUM_ADMs) are those that have more to offer (higher OCCUP_RATEs). The reason is that the supply variable OCCUP_RATE was not statistically related to NUM_ADM in any of the models in which this utilization variable was regarded as a dependent variable. However, OCCUP_RATE was statistically significant in the models in which utilization was represented by variables ToS and MEAN_COST. Specifically in models 5, 6, 8, and 9, this supply variable (OCCUP_RATE) was negatively related to utilization, indicating that the greater the supply, the lower the utilization.
After testing hypotheses, analyzing determinants in the estimated models (Fig. 3), and the data in Fig. (4), it is pos-sible to formulate the equation of a resource allocation model for Brazilian hospitals. Hence, building on Carr-Hill et al. [1] and Figs. (1, 5) show a general equation of a supply-oriented model for allocating resources to Brazilian hospitals that provide highly complex services within the SUS network. This equation is original because it considers quali-tative variables regarding the hospitals’ type (general or specialist) and their nature (public or private).
Despite the valid results (i.e., significant explicative variables) for the models that use both MEAN_COST and ToS as dependent variables, Fig. (5) adopts only the dependent utilization variable MEAN_COST (as was also done in models 6 and 9). This variable refers to the costs of the services provided and, therefore, indicates the volume of resources that are supposed to be allocated to each hospital in the sample.
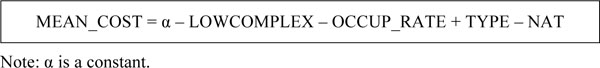
Equation for the final supply-oriented model of resource allocation.
The independent variables in Fig. (5), as well as their relationship (either positive or negative) with the dependent variable, are those statistically significant in models 6 and 9, apart from two exceptions: MGMENT and ILLIT_RATE. In such models, the three MGMENT variables were also significant conjointly, but, as previously mentioned, neither the literature nor an ad hoc analysis provides a justification for such a result. This is the reason why the three of them were not included in Fig. (5). Variable ILLIT_RATE was excluded because it is a need variable, which contradicts the proposal of a supply-oriented model, and because it was significant in only one of the nine models estimated in this study.
Some notes should be given to the formulation of the final model of resource allocation for Brazil. Carr-Hill et al. [1] propose a function to estimate a resource allocation model building on supply, demand, and utilization variables. This theoretical model is developed by drawing on the selection and estimation of such variables, which are specifically demand-oriented. In other words, the function/equation aims at estimating the different health care needs, relating them to the utilization of the health care services.
The focus of this study was on formulating a supply-oriented model that includes variables related to the hospital features – for instance, whether public, private, general, or specialist. The utilization of qualitative variables is an especially important point for the theoretical, supply-oriented model and the equation of resource allocation to Brazilian hospitals to support the reorganization of the network of highly complex health care services. In other words, drawing on such proposals (theoretical model – Fig. 1; and final model – Fig. 5), it is possible to rethink the way resources are allocated to the hospitals – whether general or specialist; public or private – as well as how to allocate them considering supply variables.
Given that the greatest MEAN_COSTs (utilization) are incurred in general hospitals (TYPE), which, in turn, are generally those with the highest OCCUP_RATEs (supply), it is possible to consider the formulation of policies to increase the supply of beds in general hospitals with a view to redistributing the number of hospital admission over several locations in Brazil. Such a redistribution is justified by the higher productivity (greater OCCUP_RATEs) of specialist hospitals, which, given the demand for highly complex services, can constitute reference centers to take care of patients living in areas where such services are not provided. Redistribution would come with a reorganization of the supply network of hospital beds.
Another issue of interest is the creation/enlargement of specialist hospitals so they can meet the demand for their specialties that are not met at public general hospitals. As mentioned before, general hospitals have greater NUM_ADMs, but, paradoxically, organizations with available beds coexist with organizations that cannot provide for those in need of inpatient health care [18]. The integration of such a service supply network at the federal level is the main topic at stake for the reorganization of the network of highly complex health care services based on the productive capacity of the hospital organizations. Such a network reorganization should include a concern with public health policy determinants, the legitimacy of formulated health policies, the creation of inter-municipal health care consortia (CIS), the structure and organization of economic, political, and social players, as well as institutional and application differences between the resource allocation models.
CONCLUDING REMARKS
It is estimated that 30% of investments in health organizations are lost through waste, rework, inefficiency, and unnecessarily complex process [19]. Despite all efforts, discussions over the need for a more rational allocation of (scarce) health care resources have found no consensus for decades. Increasing concerns over resource allocations, along with service efficiency, organization, and costs, is critical for the sector’s structure and function [7, 20].
However, full access to health care services has not yet been granted in Brazil because of the organization of the service network and the current system of resource allocation to the organizations [21]. Against this background, this paper aimed at contributing to improving public health care in Brazil by proposing a resource allocation model that can be applied to hospital organizations that provide highly complex services within the SUS network.
France [22] claims that the challenge to any national health care system is to reflect the heterogeneous needs of the various regions (and local groups) while also reducing the inequality between social actors to ensure citizenship. The present study approached the specific characteristics of the models of resource allocation and adapts the British model presented by Carr-Hill et al. [1] to construe a Brazil-specific model. It particularly approached the highly complex nature of health care services. This level of care seems to be different from the medium and especially low complexity services because of their different health policy and resource allocation orientations.
This study analyzed a sample of 251 hospitals. The results obtained in the preliminary models supported the formulation of an equation and seem to point out that, despite the sanitarians’ policy making discourse, the Brazilian resource allocation model for highly complex health care services is determined by production (supply) variables and the hospital classification (whether public or private, general or specialist).
Building on an adaptation of the Carr-Hill et al. [1] model, this study put forward a simplified theoretical model of supply (Fig. 1) to represent the relationship between utilization, supply, need, and hospital classification variables. The results of six of the nine initial models (Fig. 2) revealed the statistical significance (Fig. 3) of the supply variables (LOWCOMPLEX and OCCUP_RATE) and classification variables (TYPE and NAT) to explain the utilization of hospital services (MEAN_COST). Only model 6 revealed statistical significance for need variables (ILLIT_RATE).
However, it is once again worth mentioning the criticism in the literature to the fact that production variables determine the resources to be allocated to health care [7, 9, 11]. Despite this criticism, the present study assumes that the productive operational capacity should be the main criterion for allocating resources to hospital organizations, along with epidemiologic and socioeconomic criteria, for the sake of universality and equality.
Another relevant issue in the analysis of determinants is related to the “needs” variable. Not only is there no consensus in the literature about the best way to measure such needs, but this variable is also sensitive to different population levels when it comes to making comparisons. However, this study assumed that the hospital beds specifically provided for highly complex health care services are part of a “national” supply network, that is, the available hospital beds are (or at least should be) accessed by any individuals regardless of the municipality or state in which they are located.
In proposing/formulating a supply-oriented resource allocation model that included variables related to the hospitals’ characteristics, the results in this study may support an improved distribution/allocation of resources to Brazilian hospitals that provide highly complex health care services within the SUS network. In other words, drawing on such proposals (theoretical model – Fig. 1; and final model – Fig. 5), it is possible to rethink the way resources are allocated to hospitals – whether general or specialist; public or private – as well as the way to allocate them taking supply variables into account.
ABOUT THE AUTHORS
Mariana Guerra Associate Professor, Department of Accounting and Actuarial Sciences at the University of Brasilia. Bachelor of Science in Accounting (2008) and Master of Accounting and Control (2010) by Federal University of Minas Gerais (UFMG) and a PhD in Public Management (2013) by University of Brasilia (UNB). Member of the core research groups of Managerial and Financial Studies (NEGEC/UFMG) and Public Services Management (GESPU/UNB). Current research interests: financial and cost management, accounting and public budget, review financial performance, health economics and management of public services. She can be reached at mariguerra_mg@yahoo.com.br.
Andréa de Oliveira Gonçalves Associate Professor, Department of Accounting and Actuarial Sciences at the University of Brasilia. Ph.D. in Latin American Integration (State and Society), University of São Paulo (USP) (2005), MBA from the Federal University of Rio Grande do Sul (UFRGS) (1999) and a degree in Social Sciences from the University of Vale do Rio Doce (1993). She is an integrated member of the Center for Public Administration and Public Policy (CAPP), the Technical University of Lisbon. She has experience in Administration with an emphasis in Public Organizations, working in participatory management, public administration, entrepreneurship, local development and business administration. She can be reached at andreaegoncalves@gmail.com.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflicts of interest.
ACKNOWLEDGEMENTS
Declared none.


